Feel the Math with App Inventor
Aug 23, 2016 karen's Blog
 This is a guest blog by MIT Master Trainer Angie Zhou
This is a guest blog by MIT Master Trainer Angie Zhou
For a lot of young students, learning mathematics means rules to memorize and word problems that exist on paper. But as adults, we know having a sophisticated understanding of mathematical concepts will go a long way in understanding the world and other social and natural science subjects.
One way we can let students feel the math and play with the math is to use a simple programming tool MIT App Inventor. We can make practical application of mathematics come alive in the classrooms.
In this post, I am going to give three examples for which young students can play with various areas of mathematics, and see how it applies in real life with just a little bit of programming and lots of fun.
- Feel the calculus by drawing curved lines
- Think about probability and program a cheating die
- Understand transformation with Instagram filters
Feel the calculus
PaintPot is a beginner-level app that allows users to draw on a virtual canvas. To program drawing curved lines, students use a very interesting event-handler:
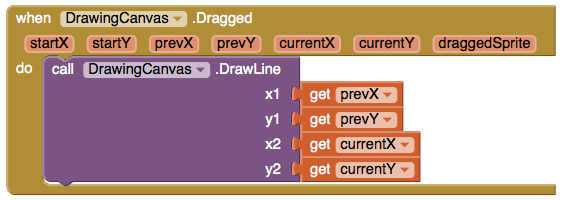
When I taught this app, many students wondered - why are we using the DrawLine function call, which draws straight lines, to draw curved lines?
I happily explained, to draw a curved line, you are really drawing lots of very small straight lines. These infinitesimal straight lines can make up curved lines.
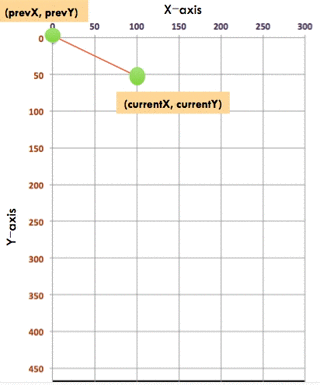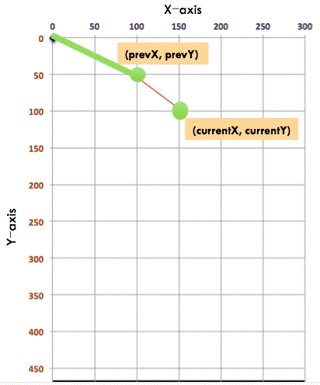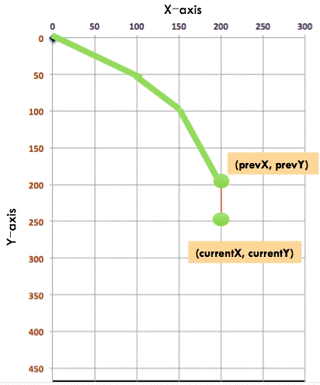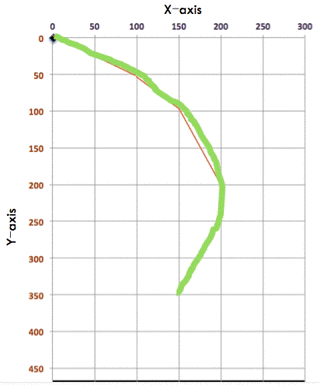
There, we are already giving students a sense of calculus without showing any equations.
Play with probability
A simple dice can be programmed using an App Inventor button.

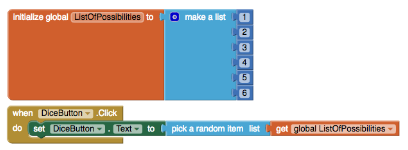
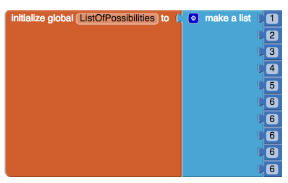
After students learn about the basic probability concepts, apart from doing word problems, they can apply their newly acquired knowledge to program something interesting - dice with various specifications. Below is the solution for a dice with six coming up half of the time.
Look at transformation
The last example is not related to App Inventor, but I put it in here because its for a relatively abstract and advanced concept that is close to students lives.
Back when I was young, transformation and matrices were just learning the rules and completing the problems, never seeing how its going to be useful. Maths teachers said they were going be useful, and I had to take their word for it.
But now, I can tell students the photo filters they have been using can be made with transformations.

Note: the formula is a hypothetical formula used to illustrate the transformation process. The real formula of a filter is most likely much more complex.
For instance, every pixel of an image can use a formula to be transformed into a different color. If you have all the formula of the pixels worked out, then you would have built the secret formula to make a photo filter.







